if you increase alpha what happens to power

Pedagogy students the concept of ability in tests of significance can be daunting. Happily, the AP Statistics curriculum requires students to understand only the concept of power and what affects it; they are not expected to compute the power of a test of significance against a particular alternate hypothesis.

What Does Power Mean?

The easiest definition for students to understand is: power is the probability of correctly rejecting the cipher hypothesis. We're typically only interested in the power of a exam when the aught is in fact faux. This definition as well makes it more clear that power is a conditional probability: the nada hypothesis makes a argument nearly parameter values, simply the power of the test is provisional upon what the values of those parameters actually are.

To make that even more clear: a hypothesis test begins with a nil hypothesis, which usually proposes a very particular value for a parameter or the departure between two parameters (for example, 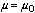 " " or "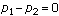").^ane And so it includes "an" alternating hypothesis, which is commonly in fact a collection of possible parameter values competing with the one proposed in the null hypothesis (for example, "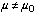" which is really a drove of possible values of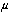, and," 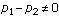which allows for many possible values of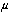. The power of a hypothesis exam is the probability of rejecting the null, simply this implicitly depends upon what the value of the parameter or the difference in parameter values really is.

The post-obit tree diagram may help students appreciate the fact that α, β, and power are all provisional probabilities.

Figure i: Reality to Decision

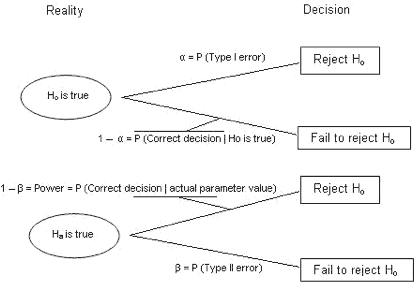
Power may be expressed in several different ways, and it might be worthwhile sharing more than than one of them with your students, as i definition may "click" with a student where another does non. Hither are a few dissimilar ways to depict what ability is:

• Power is the probability of rejecting the cypher hypothesis when in fact it is simulated.
• Power is the probability of making a right decision (to reject the nada hypothesis) when the goose egg hypothesis is simulated.
• Power is the probability that a test of significance volition pick upwardly on an result that is nowadays.
• Ability is the probability that a test of significance will detect a deviation from the null hypothesis, should such a deviation exist.
• Ability is the probability of avoiding a Type Ii error.

To aid students better grasp the concept, I continually restate what power means with unlike language each fourth dimension. For example, if nosotros are doing a test of significance at level α = 0.1, I might say, "That's a pretty big alpha level. This test is ready to reject the zilch at the drib of a chapeau. Is this a very powerful exam?" (Yeah, it is. Or at to the lowest degree, it'southward more powerful than information technology would be with a smaller alpha value.) Another example: If a student says that the consequences of a Type Ii error are very severe, then I may follow upwardly with "So you really want to avoid Type Ii errors, huh? What does that say about what we require of our examination of significance?" (We want a very powerful test.)

What Affects Ability?

There are 4 things that primarily impact the power of a examination of significance. They are:

1. The significance level α of the exam. If all other things are held constant, then equally α increases, so does the power of the examination. This is because a larger α means a larger rejection region for the test and thus a greater probability of rejecting the null hypothesis. That translates to a more powerful test. The price of this increased power is that every bit α goes up, so does the probability of a Type I fault should the nix hypothesis in fact exist true.
2. The sample size n. As n increases, so does the power of the significance test. This is because a larger sample size narrows the distribution of the examination statistic. The hypothesized distribution of the test statistic and the truthful distribution of the test statistic (should the nothing hypothesis in fact be false) become more than distinct from ane some other as they become narrower, and then information technology becomes easier to tell whether the observed statistic comes from i distribution or the other. The price paid for this increase in power is the college cost in time and resources required for collecting more data. There is commonly a sort of "point of diminishing returns" up to which it is worth the cost of the data to gain more than power, only across which the extra power is not worth the price.
3. The inherent variability in the measured response variable. As the variability increases, the power of the examination of significance decreases. One way to think of this is that a test of significance is like trying to detect the presence of a "bespeak," such as the upshot of a treatment, and the inherent variability in the response variable is "noise" that will drown out the betoken if it is too great. Researchers can't completely control the variability in the response variable, simply they can sometimes reduce information technology through especially conscientious information collection and conscientiously uniform treatment of experimental units or subjects. The design of a written report may too reduce unexplained variability, and one primary reason for choosing such a design is that it allows for increased ability without necessarily having exorbitantly costly sample sizes. For example, a matched-pairs pattern ordinarily reduces unexplained variability by "subtracting out" some of the variability that individual subjects bring to a study. Researchers may do a preliminary study before conducting a full-blown study intended for publication. There are several reasons for this, but 1 of the more than important ones is and then researchers can assess the inherent variability within the populations they are studying. An gauge of that variability allows them to determine the sample size they will require for a future test having a desired ability. A examination lacking statistical ability could easily result in a plush study that produces no significant findings.
4. The deviation between the hypothesized value of a parameter and its true value. This is sometimes called the "magnitude of the effect" in the case when the parameter of involvement is the deviation between parameter values (say, means) for 2 treatment groups. The larger the effect, the more than powerful the exam is. This is because when the effect is big, the true distribution of the examination statistic is far from its hypothesized distribution, so the ii distributions are singled-out, and it'south easy to tell which one an ascertainment came from. The intuitive idea is simply that it's easier to detect a big effect than a pocket-sized one. This principle has ii consequences that students should sympathize, and that are essentially 2 sides of the same money. On the one hand, information technology's important to understand that a subtle but important consequence (say, a modest increment in the life-saving power of a hypertension treatment) may exist demonstrable merely could require a powerful test with a large sample size to produce statistical significance. On the other hand, a small, unimportant effect may be demonstrated with a high degree of statistical significance if the sample size is large enough. Because of this, too much ability can virtually be a bad affair, at to the lowest degree then long as many people go on to misunderstand the significant of statistical significance. For your students to capeesh this aspect of power, they must understand that statistical significance is a measure of the force of evidence of the presence of an effect. It is not a measure of the magnitude of the effect. For that, statisticians would construct a conviction interval.

Two Classroom Activities

The ii activities described below are similar in nature. The start i relates power to the "magnitude of the effect," by which I mean here the discrepancy between the (cypher) hypothesized value of a parameter and its bodily value.^two The 2d one relates ability to sample size. Both are described for classes of almost twenty students, but you can modify them equally needed for smaller or larger classes or for classes in which y'all have fewer resource available. Both of these activities involve tests of significance on a single population proportion, merely the principles are true for nearly all tests of significance.

Activity ane: Relating Power to the Magnitude of the Issue

In advance of the grade, y'all should ready 21 bags of poker fries or some other token that comes in more than one color. Each of the numberless should have a dissimilar number of bluish chips in it, ranging from 0 out of 200 to 200 out of 200, past 10s. These bags represent populations with unlike proportions; label them by the proportion of blueish chips in the bag: 0 per centum, five percent, 10 per centum,... , 95 percent, 100 percentage. Distribute ane bag to each student. Then instruct them to shake their bags well and draw xx fries at random. Have them count the number of blueish chips out of the 20 that they observe in their sample and so perform a test of significance whose goose egg hypothesis is that the bag contains 50 pct blue chips and whose alternate hypothesis is that information technology does not. They should apply a significance level of α = 0.10. It'southward fine if they apply engineering to do the computations in the test.

They are to record whether they rejected the zippo hypothesis or not, then replace the tokens, shake the bag, and repeat the simulation a full of 25 times. When they are washed, they should compute what proportion of their simulations resulted in a rejection of the null hypothesis.

Meanwhile, draw on the board a pair of axes. Characterization the horizontal axis "Actual Population Proportion" and the vertical axis "Fraction of Tests That Rejected."

When they and you are washed, students should come to the board and describe a signal on the graph corresponding to the proportion of blue tokens in their bag and the proportion of their simulations that resulted in a rejection. The resulting graph is an approximation of a "power curve," for power is precisely the probability of rejecting the null hypothesis.

Figure ii is an example of what the plot might look like. The lesson from this action is that the power is affected by the magnitude of the difference between the hypothesized parameter value and its true value. Bigger discrepancies are easier to detect than smaller ones.

Figure two: Power Bend

Activity two: Relating Power to Sample Size

For this activity, ready 11 paper bags, each containing 780 blue fries (65 pct) and 420 nonblue chips (35 percentage).ⁱⁱⁱ This action requires 8,580 blue chips and 4,620 nonblue chips.

Pair up the students. Assign each student pair a sample size from 20 to 120.

The activeness gain as did the last one. Students are to have 25 samples corresponding to their sample size, recording what proportion of those samples lead to a rejection of the aught hypothesis p = 0.five compared to a two-sided alternative, at a significance level of 0.10. While they're sampling, you make axes on the lath labeled "Sample Size" and "Fraction of Tests That Rejected." The students put points on the lath every bit they complete their simulations. The resulting graph is a "power curve" relating power to sample size. Below is an example of what the plot might look like. Information technology should show conspicuously that when p = 0.65 , the goose egg hypothesis of p = 0.50 is rejected with a higher probability when the sample size is larger.

(If you do both of these activities with students, information technology might be worth pointing out to them that the indicate on the kickoff graph corresponding to the population proportion p = 0.65 was estimating the same ability as the betoken on the second graph corresponding to the sample size n = 20.)

Conclusion

The AP Statistics curriculum is designed primarily to help students understand statistical concepts and become critical consumers of information. Being able to perform statistical computations is of, at most, secondary importance and for some topics, such as power, is not expected of students at all. Students should know what power ways and what affects the power of a test of significance. The activities described above can help students understand ability better. If you teach a 50-minute form, y'all should spend one or at most ii form days education power to your students. Don't get bogged down with calculations. They're important for statisticians, but they're best left for a later course.

Notes

1. Of the hypothesis tests in the AP statistics curriculum, of which but the chi-square tests do non involve a null that makes a statement about one or two parameters. For the balance of this article, I write as though the zilch hypothesis were a statement about 1 or ii parameter values, such as 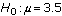or
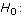
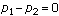
2. In the context of an experiment in which one of two groups is a control grouping and the other receives a treatment, and so "magnitude of the event" is an apt phrase, as information technology quite literally expresses how large an impact the treatment has on the response variable. Simply hither I utilize the term more generally for other contexts too.
3. I know that'southward a lot of chips. The reason this activity requires and then many chips is that information technology is a good idea to adhere to the so-called "ten per centum dominion of thumb," which says that the standard mistake formula for proportions is approximately correct so long as your sample is less than 10 percent of the population. The largest sample size in this activity is 120, which requires 1,200 chips for that educatee's purse. With smaller sample sizes you could get abroad with fewer chips and nevertheless adhere to the 10 percent rule, but it'south important in this activity for students to empathize that they are all essentially sampling from the same population. If they perceive that some bags comprise many fewer fries than others, you may cease upward in a word yous don't want to accept, virtually the fact that only the proportion is what'south of import, not the population size. It'southward probably easier to just seize with teeth the bullet and fix bags with a lot of chips in them.

jacobswhought.blogspot.com

Source: https://apcentral.collegeboard.org/courses/ap-statistics/classroom-resources/power-in-tests-of-significance

Share this post